As an example, we can examine the European roulette model (roulette with one zero). Since this roulette has 37 cells with equal odds of hitting, it is clear that this is a final model of field probability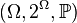 
, where 
, 
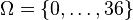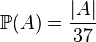for all 
. We'll call the bet S a three (A,r,ξ), where A for a certain random event|event 
, and 
= random size. The event A naturally leads to a winning event, r to the size of the bet (in dollars, for example), ξ to the bet rule, and the mathematical expectation M[ξ] relates to the bet profitability.
The rules of European roulette have 10 types of bets. First we can examine the 'Straight Up' bet. It's clear that in this case, 
, where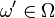 
, and ξ is determined by this law
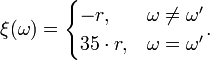
The bet's probability is equal to
![M[\xi] =
\frac{1}{37} \sum_{\omega \in \Omega} \xi(\omega) =
\frac{1}{37} \left(\xi(\omega^\prime) +
\sum_{\omega \ne \omega^\prime} \xi(\omega)\right) =
\frac{1}{37} \left(35 \cdot r - 36 \cdot r \right) = -\frac{r}{37}
\approx -0.027r.](http://upload.wikimedia.org/math/a/1/c/a1c4a05105447575136f448fd8860fa7.png)
Without details, for a bet, red or black, the rule is determined as
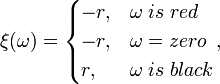
and the profitability
![M[\xi] = \frac{1}{37}(18 \cdot r - 18 \cdot r - r) = -\frac{r}{37}](http://upload.wikimedia.org/math/f/5/a/f5a95373f6ccb30fc39795fcbadc5bf0.png)
. For similar reasons it is simple to see that the profitability if also equal for all remaining types of bets.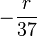 
.[6][7]In reality this means that, the more bets a player makes, the more he is going to lose independent of the strategies (combinations of bet types or size of bets) that he employs:
![\sum_{n = 1}^{\infty}M[\xi_n] = -\frac{1}{37}\sum_{n = 1}^{\infty}r_n = -\infty.](http://upload.wikimedia.org/math/9/6/f/96fba465aeb29fb7086f9bf398e7a823.png)
Here, the profit margin for the roulette owner is equal to approximately 2.7%. Nevethless, several roulette strategy systems have been developed despite the losing odds.[8]
It's worth noting that the odds for the player in American roulette are even worse, as the bet profitability is
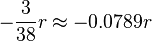, and the rest are 
.
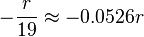0 comments:
Post a Comment